Logarithme népérien – Logarithme décimal : Cours-Résumés-TD-TP-Examens-Exercices corrigés
Logarithme népérien – Logarithme décimal : Cours, Résumé et exercices corrigés
A- Logarithme_népérien
1- Définition
La fonction logarithme népérien, notée ln, est l’unique primitive de la fonction x → 1/x définie sur ] 0 ; +∞ [ qui s’annule en 1.
La fonction ln est la fonction réciproque de la fonction exponentielle x = ey ⇔ y = ln x
2- Représentation
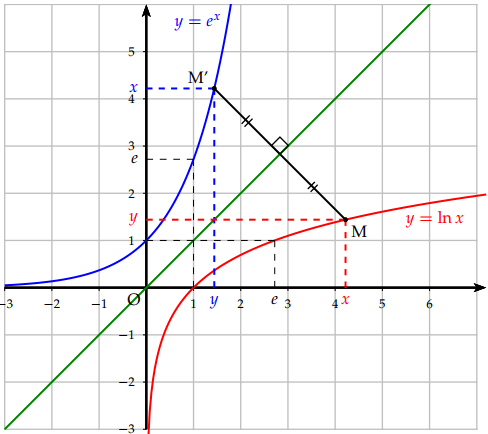
Les représentations de la fonction logarithme népérien et de la fonction exponentielle sont symétriques par rapport à la droite d’équation y = x.
Les fonctions exp et ln sont des fonctions réciproques l’une de l’autre.
3- Propriétés de la fonction logarithme népérien
- La fonction ln est définie sur l’intervalle ]0;+∞[
- ln(1) = 0
- Pour tout réel x > 0, ln′(x) = 1/x
- Pour tous nombres réels a et b strictement positifs, on a : ln(a × b) = ln(a)+ln(b)
- Pour tout nombre réel strictement positif a, ln(1/a) = −ln(a)
- Pour tous nombres réels strictement positifs a et b, ln(a/b) = ln(a)−ln(b)
- Pour tout nombre réel strictement positif a, et pour tout entier relatif n, ln(an) = n ln(a)
- Pour tout nombre réel strictement positif a,
ln(\sqrt{a})=\frac{1}{2}ln(a)4- Etude de la fonction logarithme_népérien
4-1. Domaine de définition
- Le domaine de définition de la fonction logarithme est D =]0;+∞[
- Ainsi, dans le cas d’une fonction de la forme f = ln(u), le domaine de définition est donné par les solutions de l’inéquation u(x) > 0.
4-2. Variation de la fonction logarithme_népérien
La fonction logarithme népérien est continue et strictement croissante sur ]0;+∞[ .
Démonstration
- La fonction ln est dérivable sur ]0;+∞[ donc continue sur cet intervalle.
- La dérivée de la fonction ln est la fonction définie sur ]0;+∞[ par ln′(x) = 1/x. Or si x > 0 alors, 1/x> 0. La dérivée de la fonction ln est strictement positive, donc la fonction ln est strictement croissante sur ]0;+∞[
On déduit de ce théorème les propriétés suivantes :
Pour tous réels a et b strictement positifs :
- ln(a) = ln(b) si, et seulement si, a = b
- ln(a) > ln(b) si, et seulement si, a > b
En particulier, puisque ln1 = 0 :
Pour tout réel x strictement positif :
- lnx = 0 si, et seulement si, x = 1
- lnx > 0 si, et seulement si, x > 1
- lnx < 0 si, et seulement si, 0 < x < 1
4-3. Limites de la fonction logarithme népérien
- La fonction ln a pour limite +∞ en +∞ :
\lim_{x\rightarrow +\infty }x=+\infty - La fonction ln a pour limite -∞ en 0 :
\lim_{x\rightarrow 0}x=-\infty L’axe des ordonnées est asymptote verticale à la courbe d’équation y = lnx
B- Logarithme décimal
La fonction logarithme_népérien est particulièrement intéressante du fait de sa propriété de transformation d’un produit en somme. Mais comme on utilise, pour écrire les nombres, le système décimal, on lui préfère parfois une autre fonction possédant la même propriété de transformation de produit en somme mais prenant la valeur 1 lorsque x = 10 (et donc la valeur 2 lorsque x = 100, la valeur 3 lorsque x = 1000 etc…)
Cette fonction sera appelée fonction logarithme décimal ou fonction logarithme de base 10.
1. Définition de Logarithme décimal
On appelle fonction logarithme décimal et on note log la fonction définie sur ] 0 ; +∞ [ par : log (x)=ln (x)/ln (10)
2. Propriétés de Logarithme décimal
- log 1 = 0 et log 10 = 1
- Pour tous réels a et b strictement positifs on a :
- log ( a × b ) = log a + log b ;
- log 1/a = – log a ;
- log a/ b = log a – log b ;
- log a½ = (½) log a
- Pour tout n ∈ Z, log a n = n log a
3. Remarques :
La fonction logarithme décimal étant définie par log x = k × ln x avec k = 1/ln 10. Il est facile d’étudier ses variations et de donner sa courbe représentative.
Soit a un réel strictement positif tel que a ≠ 1 . On définit de manière analogue la fonction logarithme de base a, notée log a : loga(x)=log(x)/log(a)
Pour plus de détails télécharger les documents ci-dessous:
Liens de téléchargement des cours sur Logarithme népérien
Cours sur Logarithme népérien N°1
Cours sur Logarithme népérien N°2
Cours sur Logarithme_népérien N°3
Cours sur Logarithme_népérien N°4
Cours sur Logarithm_ népérien N°5
Cours sur Logarithme_népérien N°6
Cours sur Logarithme_népérien N°7
Liens de téléchargement des résumés sur Logarithme népérien
Résumé sur Logarithme népérien N°1
Résumé sur Logarithme_népérien N°2
Résumé sur Logarithme_népérien N°3
Résumé sur Logarithme_népérien N°4
Liens de téléchargement des exercices corrigés sur Logarithme népérien
Exercices corrigés sur Logarithme népérien N°1
Exercices corrigés sur Logarithme_népérien N°2
Exercices corrigés sur Logarithme_népérien N°3
Exercices corrigés sur Logarithme_népérien N°4
